Implementing AES From Scratch

The AES algorithm is widely used today, whether it’s for encrypting a connection to a website, encrypting data on your hard drive, or storing passwords in your favorite password manager. It has been battle-tested for many decades and is still recommended as one of the most secure algorithms.

In this article, I explain how AES encryption works and how the algorithm is implemented.

The Cipher

There are two fundamental properties that make a cipher secure:

• Diffusion which is about hiding the statistical relationship between the ciphertext and the plaintext. If even a single bit is changed in the plaintext, the cipher should change completely.
• Confusion which is about complicating the relationship between the key and the ciphertext with the aim of making cryptanalysis more challenging.

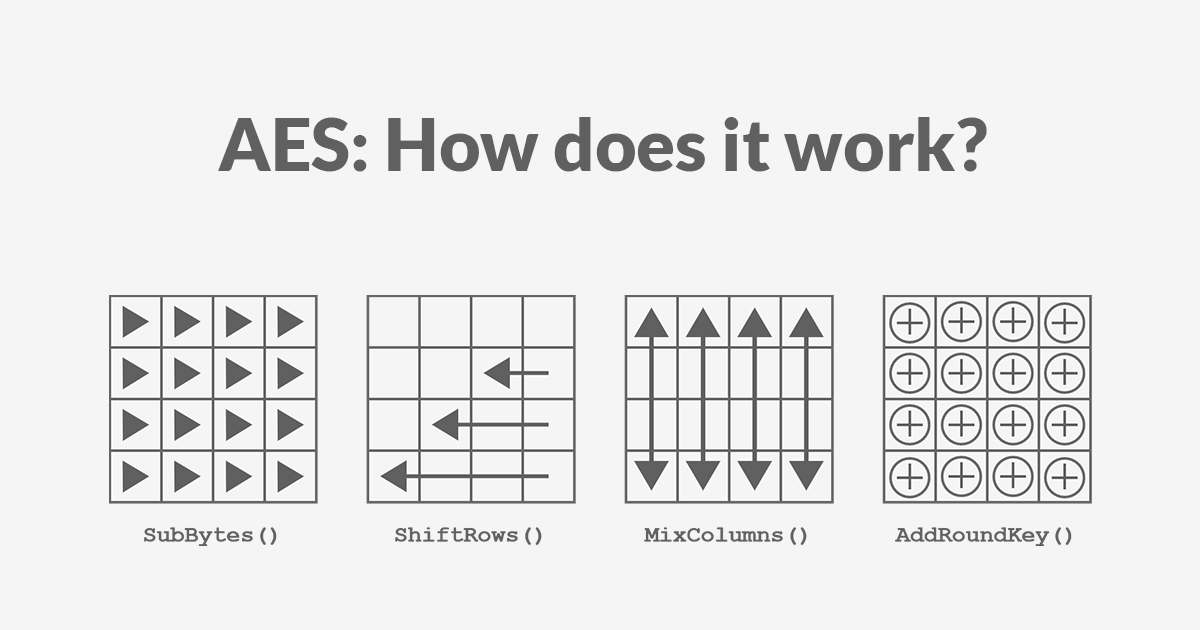
AES encryption consists of 4 “simple” steps that are repeated for several rounds. Each step on its own doesn’t significantly enhance the algorithm’s security, but by repeating all these steps together multiple times, we increase both the confusion and the diffusion.

The number of rounds depends on the key size, allowing a trade-off between performance and security.

Key Length (bits)	Number of Rounds
128	10
192	12
256	14

Each of these steps operates on a block of exactly 16 bytes called the state, which is represented as a 4x4 array:

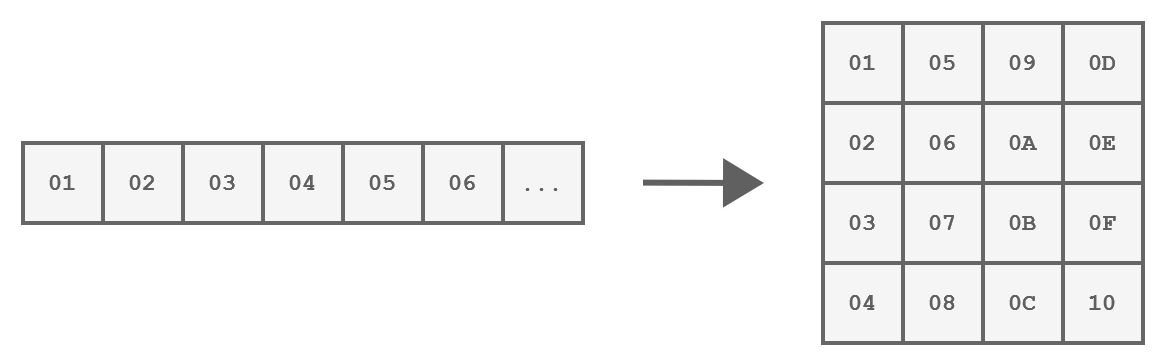How a block of 16 bytes is represented

These steps are:

1. SubBytes
2. ShiftRows
3. MixColumns
4. AddRoundKey

And those operations are implemented in the following way. We start with an initial AddRoundKey, and then we perform each round. In the last round, the MixColumns step is omitted.

void aes_cipher_block(AesContext *ctx, uint8_t block[4][4])
{
    // Initial AddRoundKey
    add_round_key(block, ctx->round_key);

    // Iterate through each round
    for (int round = 1; round < ctx->number_of_round; round++)
    {
        sub_bytes(block);
        shift_rows(block);
        mix_columns(block);
        add_round_key(block, ctx->round_key + round * 4);
    }

    // Final round without MixColumns
    sub_bytes(block);
    shift_rows(block);
    add_round_key(block, ctx->round_key + ctx->number_of_round * 4);
}

To understand these operations better, let’s take a closer look at each step.

The SubBytes Step

This step is a byte substitution operation that operates on each byte of the state, using a predefined substitution table known as the S-Box. The purpose of SubBytes is to introduce non-linearity and confusion into the data.

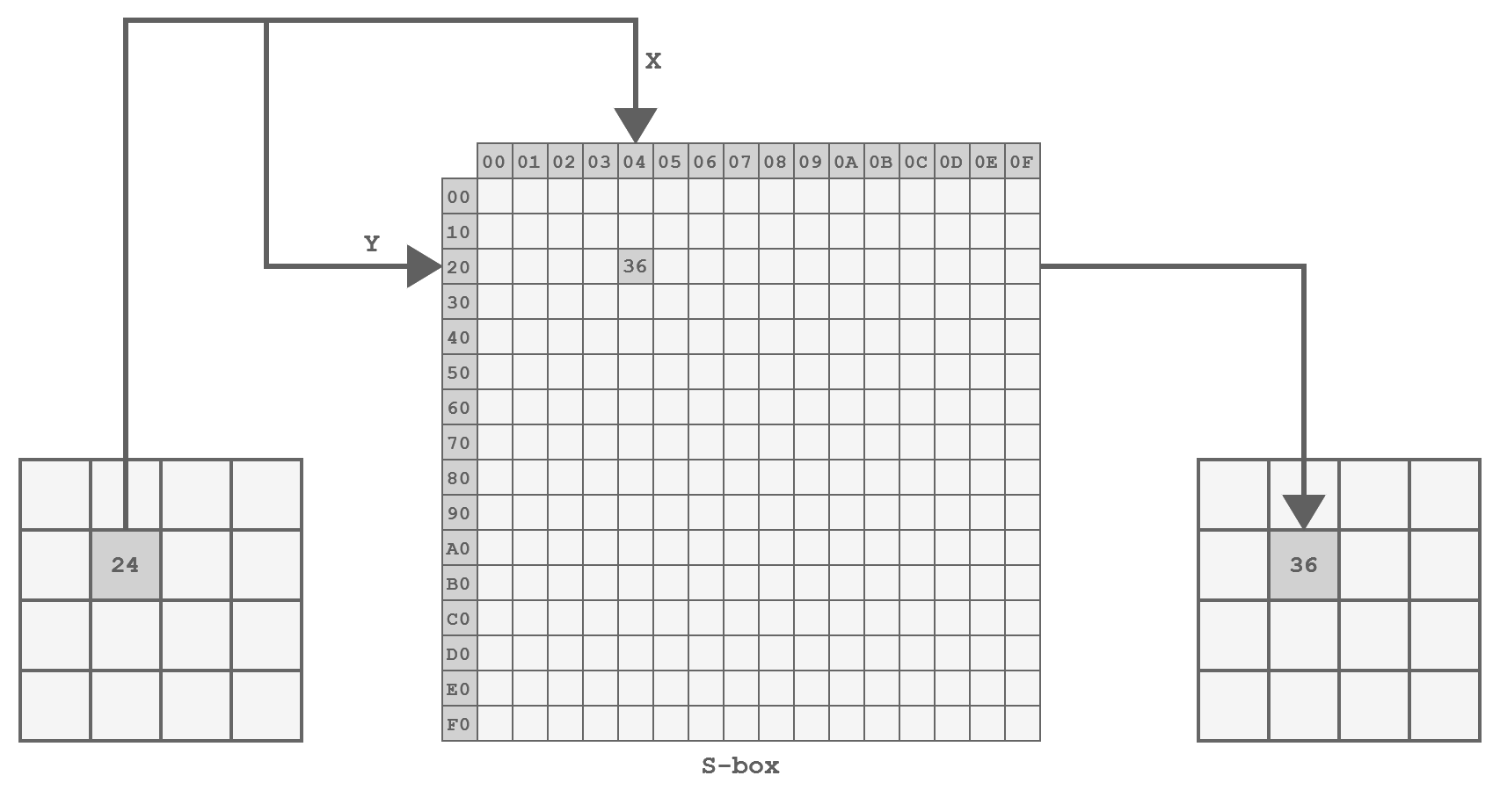Representation of the SubBytes step

The implementation is straightforward, involving a lookup into a hardcoded table, as follows:

// The S-Box
static const uint8_t substitution_box[256] = {
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16};

// Performs the SubBytes step 
void sub_bytes(uint8_t block[4][4])
{
    // Substitute each byte using the S-Box
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 4; j++)
            block[j][i] = substitution_box[block[j][i]];
}

The ShiftRows Step

In this step, the bytes within each row of the state are shifted to the left:

• The first row is not touched
• The second row is shifted one position to the left
• The third row is shifted two positions to the left
• The fourth row is shifted three positions to the left.

This operation helps achieve diffusion by spreading bytes across the block.

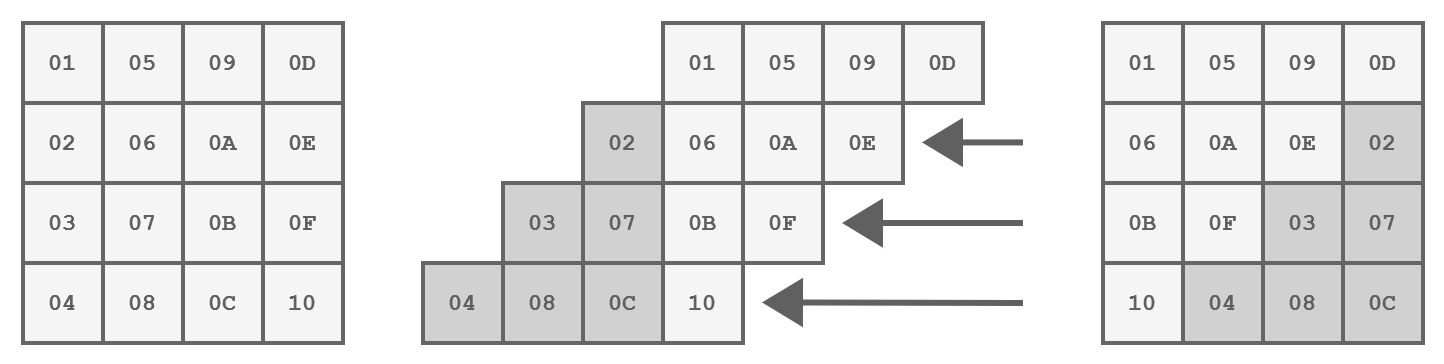Representation of the ShiftRows step

The code for this step is implemented as follows:

// Performs the ShiftRows step 
void shift_rows(uint8_t block[4][4])
{
    uint8_t temp;

    // Shift the second row one position to the left
    temp = block[0][1];
    block[0][1] = block[1][1];
    block[1][1] = block[2][1];
    block[2][1] = block[3][1];
    block[3][1] = temp;

    // Shift the third row two positions to the left (by swapping byte 1 and 3, then byte 2 and 4)
    temp = block[0][2];
    block[0][2] = block[2][2];
    block[2][2] = temp;
    temp = block[1][2];
    block[1][2] = block[3][2];
    block[3][2] = temp;

    // Shift the fourth row three positions to the left (or one position to the right)
    temp = block[3][3];
    block[3][3] = block[2][3];
    block[2][3] = block[1][3];
    block[1][3] = block[0][3];
    block[0][3] = temp;
}

The MixColumns Step

This is the most complex step because it performs mathematical operations in the Galois field, where values range from 0 to 255. This means that standard operations like addition and multiplication are implemented differently.

The addition is simply a XOR operation, but the multiplication is much more complex:

// Multiplication in the Galois field
uint8_t mul(uint8_t a, uint8_t b) 
{
    uint8_t result = 0; 

    while (b != 0) 
    {
        if (b & 1) 
            result ^= a;

        if (a & 0x80)
            a = (a << 1) ^ 0x11b; 
        else
            a <<= 1; 

        b >>= 1;
    }

    return result;
}

The MixColumns step involves multiplying each column individually by a matrix. This has the effect of replacing each byte with a value that depends on all the other bytes in the column increasing the diffusion.

\[\begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \\ \end{bmatrix} \times \begin{bmatrix} a0 \\ a1 \\ a2 \\ a3 \\ \end{bmatrix}\]

If we implement the matrix multiplication as is, we get a function similar to this:

// Performs the MixColumns step 
void mix_columns(uint8_t block[4][4])
{
    // Iterate through each column
    for (int i = 0; i < 4; i++)
    {
        uint8_t a0 = block[i][0];
        uint8_t a1 = block[i][1];
        uint8_t a2 = block[i][2];
        uint8_t a3 = block[i][3];

        // Perform the matrix multiplication 
        block[i][0] = mul(2, a0) ^ mul(3, a1) ^ a2 ^ a3;
        block[i][1] = a0 ^ mul(2, a1) ^ mul(3, a2) ^ a3;
        block[i][2] = a0 ^ a1 ^ mul(2, a2) ^ mul(3, a3);
        block[i][3] = mul(3, a0) ^ a1 ^ a2 ^ mul(2, a3);
    }
}

However, there is a much more efficient way to implement MixColumns as proposed by the algorithm’s author. Instead, we will define a function xtime(x) that corresponds to the multiplication by the constant 2 in the Galois field.

// Calculates the multiplication of a byte with 2 in the Galois field.
uint8_t xtime(uint8_t byte)
{
    if (byte & 0x80)
        return (byte << 1) ^ 0x1B;
    else 
        return byte << 1;
}

// Performs the MixColumns step 
void mix_columns(uint8_t block[4][4])
{
    uint8_t xored_column;
    uint8_t temp;

    // Iterate through each column
    for (int i = 0; i < 4; i++)
    {
        // XOR of all bytes in the column
        xored_column = block[i][0] ^ block[i][1] ^ block[i][2] ^ block[i][3];

        temp = block[i][0];

        // Perform some magic equivalent to the matrix multiplication
        block[i][0] ^= xtime(block[i][0] ^ block[i][1]) ^ xored_column;
        block[i][1] ^= xtime(block[i][1] ^ block[i][2]) ^ xored_column;
        block[i][2] ^= xtime(block[i][2] ^ block[i][3]) ^ xored_column;
        block[i][3] ^= xtime(block[i][3] ^ temp) ^ xored_column;
    }
}

The AddRoundKey Step

In this step, the encryption key is incorporated into the state using a simple bitwise XOR operation:

// Performs the AddRoundKey step
void add_round_key(uint8_t block[4][4], uint8_t key[4][4])
{
    // XOR each byte with the key
    for (int i = 0; i < 4; i++)
        for (int j = 0; j < 4; j++)
            block[j][i] ^= key[j][i];
}

The Key Expansion

When applying the key in each round, it’s important to always use a different key. That’s why the cipher key isn’t used directly but rather a round key. These round keys are generated at the very beginning of the process by expanding the cipher key.

The expanded key can be viewed as a multidimensional array with 4 columns, created by combining two previous rows using XOR operations.

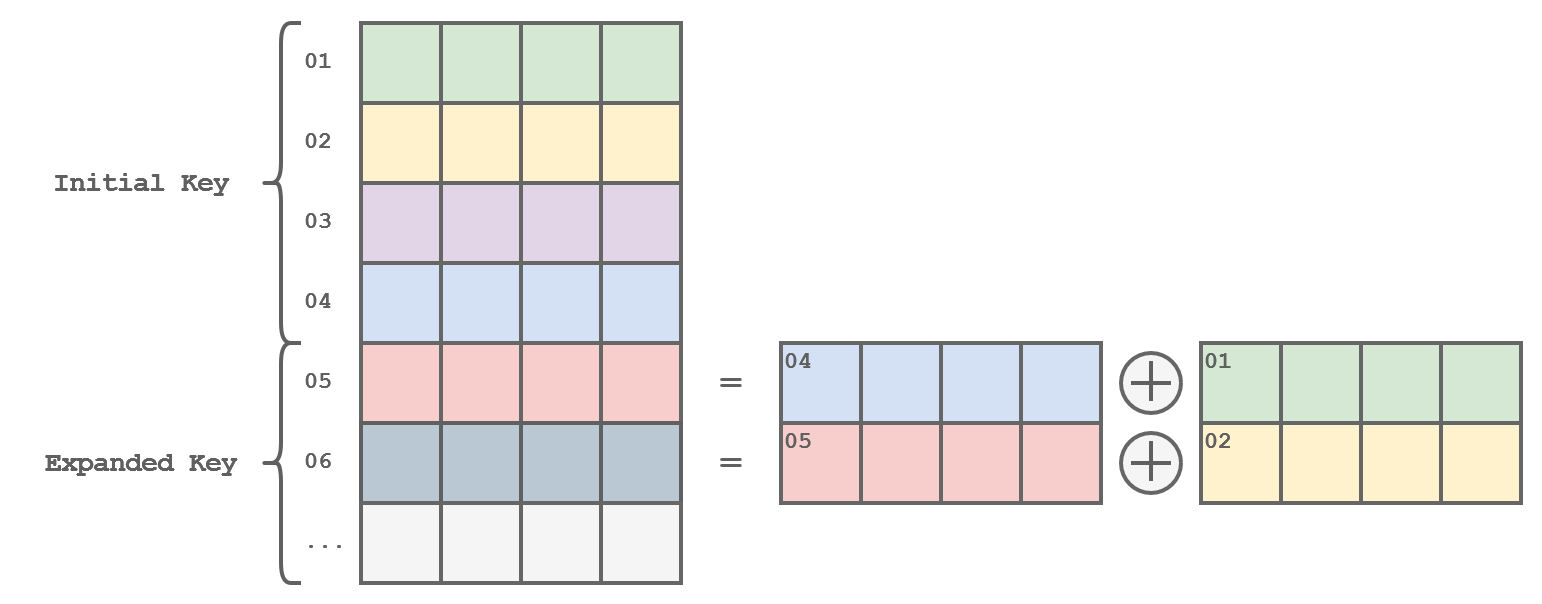Representation of the Key Expansion

The function would be implemented this way, but we are still missing some important steps.

const int keysize_words = keysize_bytes / 4;
const int expanded_keysize = 4 * (ctx->number_of_round + 1);

for (int i = keysize_words; i < expanded_keysize; i++)
{
    ctx->round_key[i][0] = ctx->round_key[i - 1][0] ^ ctx->round_key[i - keysize_words][0];
    ctx->round_key[i][1] = ctx->round_key[i - 1][1] ^ ctx->round_key[i - keysize_words][1];
    ctx->round_key[i][2] = ctx->round_key[i - 1][2] ^ ctx->round_key[i - keysize_words][2];
    ctx->round_key[i][3] = ctx->round_key[i - 1][3] ^ ctx->round_key[i - keysize_words][3];
}

Every time we have generated a complete new key (of the same size as the initial key), we need to apply some transformations to the next row:

1. Shift the row one byte to the left
2. Substitute each byte using the S-Box
3. XOR the first byte with a value that varies with each iteration.

if (i % keysize_words == 0)
{
    rot_word(previous);
    sub_word(previous);
    previous[0] ^= round_constant[i / keysize_words];
}

If the key is 32 bytes (AES-256), an additional step (SubWord) must be added half way before the previous transformation.

if (keysize_bytes == 32 && i % keysize_words == 4)
{
    sub_word(previous);
}

Here is the complete function:

static const uint8_t round_constant[32] = { 0x7d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36};

// Performs the key expansion for AES encryption
void aes_key_expansion(AesContext *ctx, uint8_t *key, size_t keysize_bytes)
{
    // Calculate the number of words in the key
    const int keysize_words = keysize_bytes / 4;

    // Calculate the final size of the expanded key
    const int expanded_keysize = 4 * (ctx->number_of_round + 1);

    // Copy the original key to the initial part of the round key
    memcpy(ctx->round_key, key, keysize_bytes);

    for (int i = keysize_words; i < expanded_keysize; i++)
    {
        // The previous word
        uint8_t previous[4] = {ctx->round_key[i - 1][0], ctx->round_key[i - 1][1], ctx->round_key[i - 1][2], ctx->round_key[i - 1][3]};

        if (i % keysize_words == 0)
        {
            // It's time to apply some transformation 
            rot_word(previous);
            sub_word(previous);
            previous[0] ^= round_constant[i / keysize_words];
        }
        else (keysize_bytes == 32 && i % keysize_words == 4)
        {
            // Additional step for 256 bit keys
            sub_word(previous);
        }

        // Generate the next word in the round key by XORing 2 previous rows
        ctx->round_key[i][0] = previous[0] ^ ctx->round_key[i - keysize_words][0];
        ctx->round_key[i][1] = previous[1] ^ ctx->round_key[i - keysize_words][1];
        ctx->round_key[i][2] = previous[2] ^ ctx->round_key[i - keysize_words][2];
        ctx->round_key[i][3] = previous[3] ^ ctx->round_key[i - keysize_words][3];
    }
}

// Substitute each byte using the S-Box
void sub_word(uint8_t word[16])
{
    for (int i = 0; i < 16; i++)
        word[i] = substitution_box[word[i]];
}

// Shift the bytes to the left
void rot_word(uint8_t word[16])
{
    const uint8_t tmp = word[0];
    word[0] = word[1];
    word[1] = word[2];
    word[2] = word[3];
    word[3] = tmp;
}

Mode of operation

So far, we’ve explored how AES encrypts individual blocks of data. However, for practical applications like encrypting files, different modes of operation are needed to handle data bigger than 16 bytes.

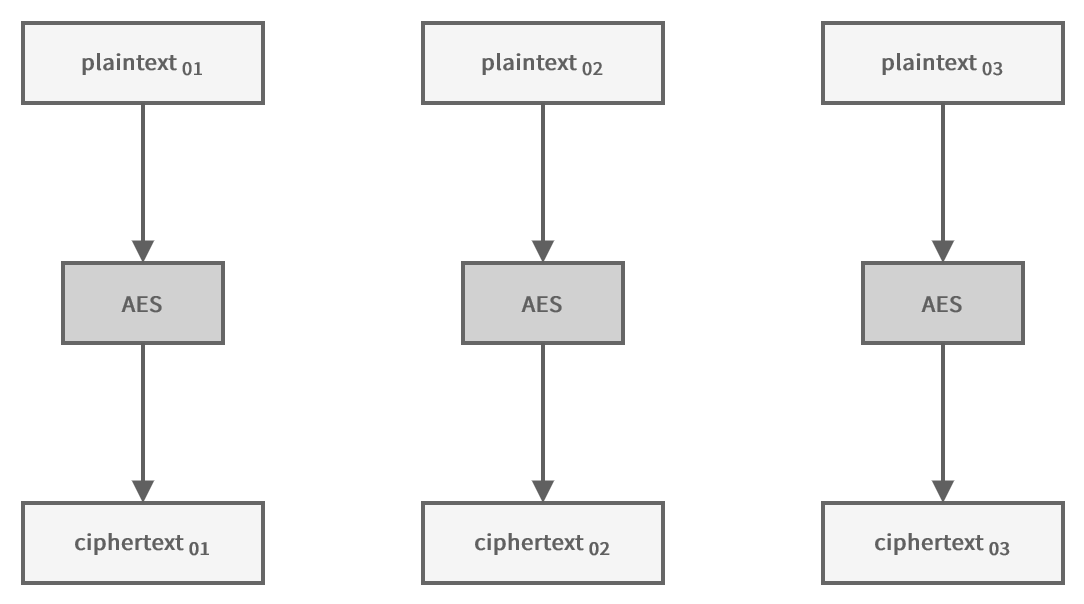
Electronic Code Book (ECB)

The simplest mode of operation is the Electronic Codebook (ECB), which involves dividing the message into several blocks. Each block is then simply encrypted using the process we’ve seen.

Electronic Code Book (ECB)

If necessary, padding is added to the last block to ensure that all blocks are of a size of 16 bytes. Padding is achieved by adding bytes until the last block reaches the desired size. The value of the added bytes is equal to the number of bytes added. So, if the last block is composed of 11 bytes, you need to add the value 0x05 five times.

PKCS#7 padding of a 11 bytes block

// Pad the plaintext in preparation for AES encryption
size_t aes_pad_plaintext(uint8_t **buffer, size_t size)
{
    // Calculate the amount of padding bytes required
    uint8_t padding = 16 - (size % 16);

    // Reallocate a new block of memory with padding
    *buffer = realloc(*buffer, size + padding);

    // Fill the padding bytes with the padding value
    memset(*buffer + size, padding, padding);

    // Return the new reallocated size
    return size + padding;
}

Here’s how ECB is implemented:

// AES encryption using the Electronic Code Book (ECB) mode.
void aes_ecb_encrypt(AesContext *ctx, uint8_t *buffer, size_t size)
{
    // Iterate through the data in blocks of 16 bytes
    for (int i = 0; i < size; i += 16)
        // Perform AES encryption on the current block
        aes_cipher_block(ctx, buffer + i);
}

The issue with this mode of operation is that every identical block will be encrypted exactly the same way. The property of diffusion is completely lost, and it’s possible to detect certain patterns in the encrypted message.

A good way to visualize the impact of this problem is to encrypt the raw data of an image:

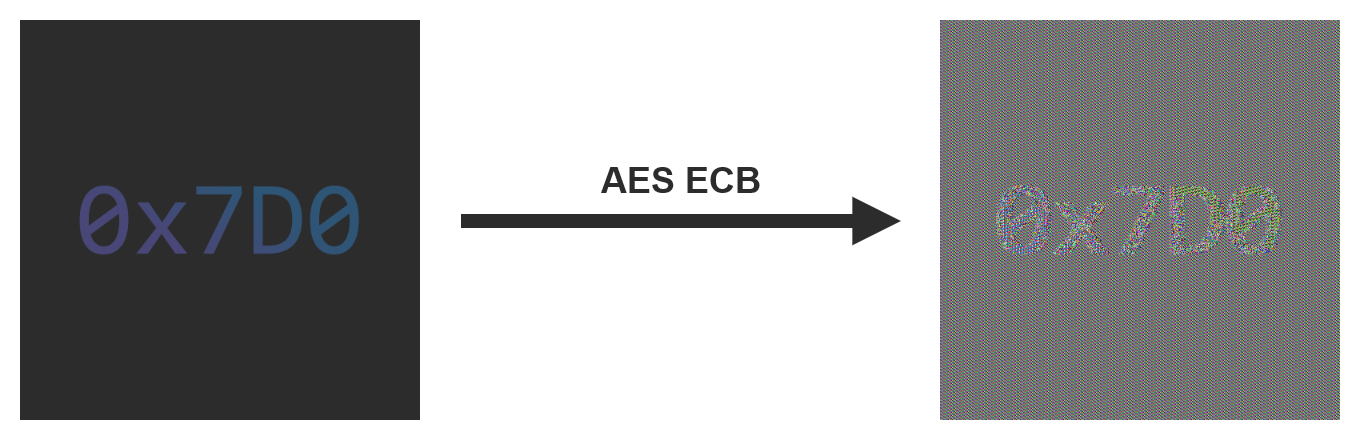An example of encryption using the ECB mode

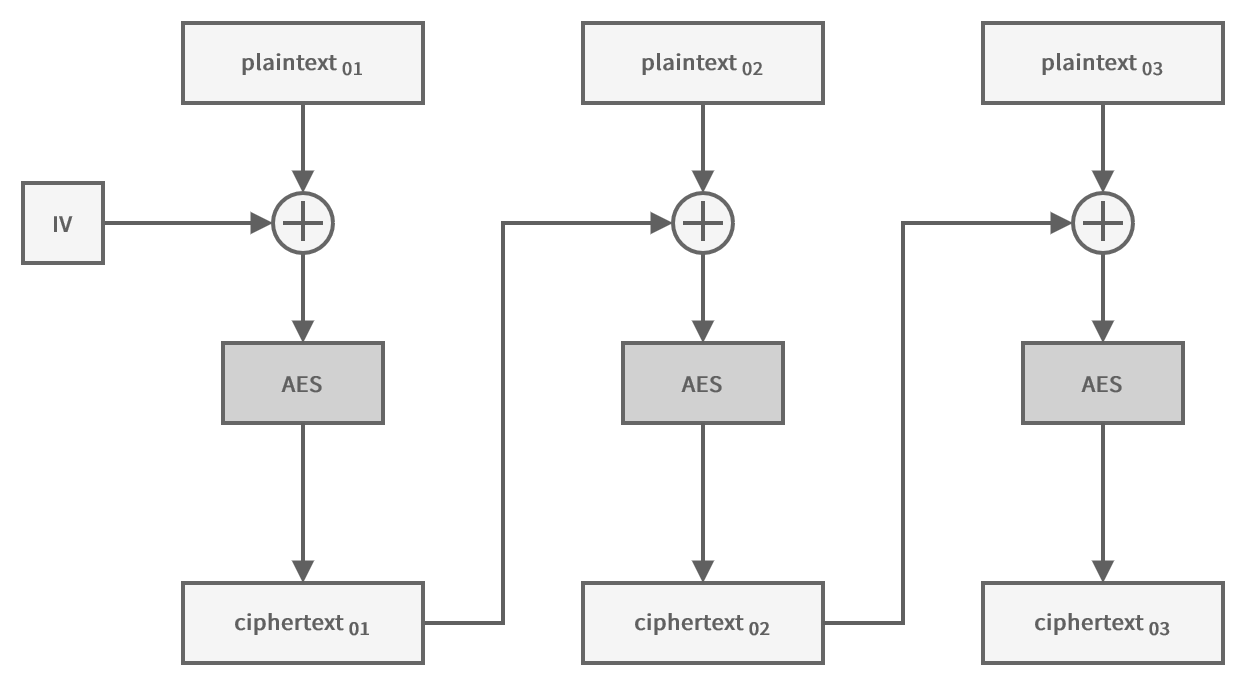
Cipher Block Chaining (CBC)

To counter the security issues of Electronic Codebook (ECB), you need a mode of operation that always produces different encrypted blocks. Cipher Block Chaining (CBC) is a simple way to meet this criterion. Each block is XORed with the previously encrypted block before itself being encrypted. As the name of the mode implies, you can think of it as a chain where each block depends on the last one.

Cipher Block Chaining (CBC)

// AES encryption using the Cipher Block Chaining (CBC) mode.
void aes_cbc_encrypt(AesContext *ctx, uint8_t *buffer, size_t size)
{
    // IV is used for the first block
    uint8_t *previous = ctx->initialization_vector;

    // Iterate through the data in blocks of 16 bytes
    for (int i = 0; i < size; i += 16)
    {
        // XOR the current block of plaintext with the previous ciphertext block
        for (int j = 0; j < 16; j++)
            buffer[i + j] ^= previous[j];

        // Perform AES encryption on the current block
        aes_cipher_block(ctx, (buffer + i));

        // Update the previous pointer
        previous = buffer + i;
    }
}

To encrypt the first block of data, you need an initialization vector (IV) of the same size as a block. This IV can be distributed in clear text along with the ciphertext, but it must be unpredictable and unique. Therefore, it’s recommended to use a random value.

If we take the same image and encrypt it this time using the CBC mode, it’s not possible to discern a specific pattern, unlike the ECB mode.

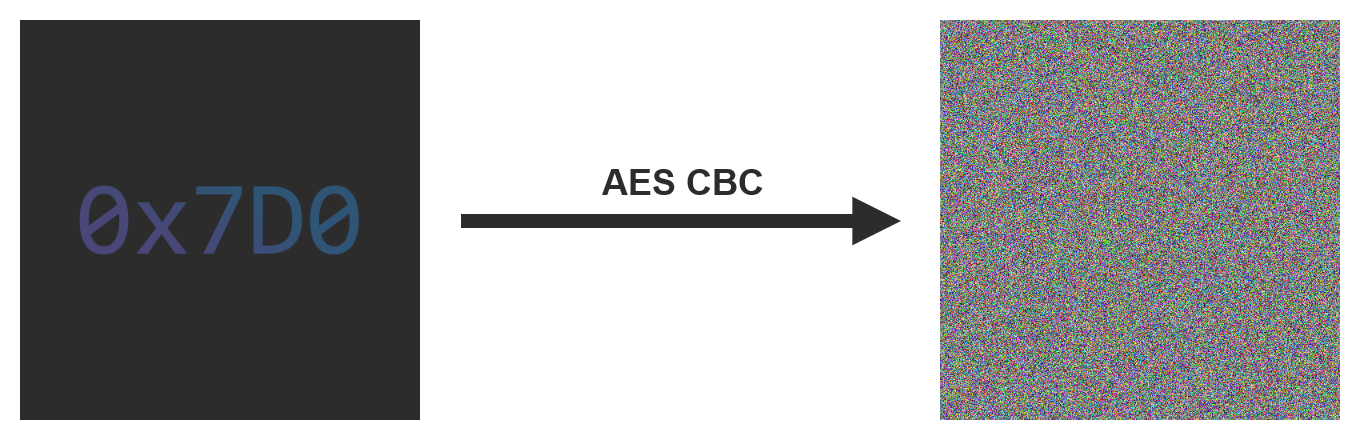An example of encryption using the CBC mode

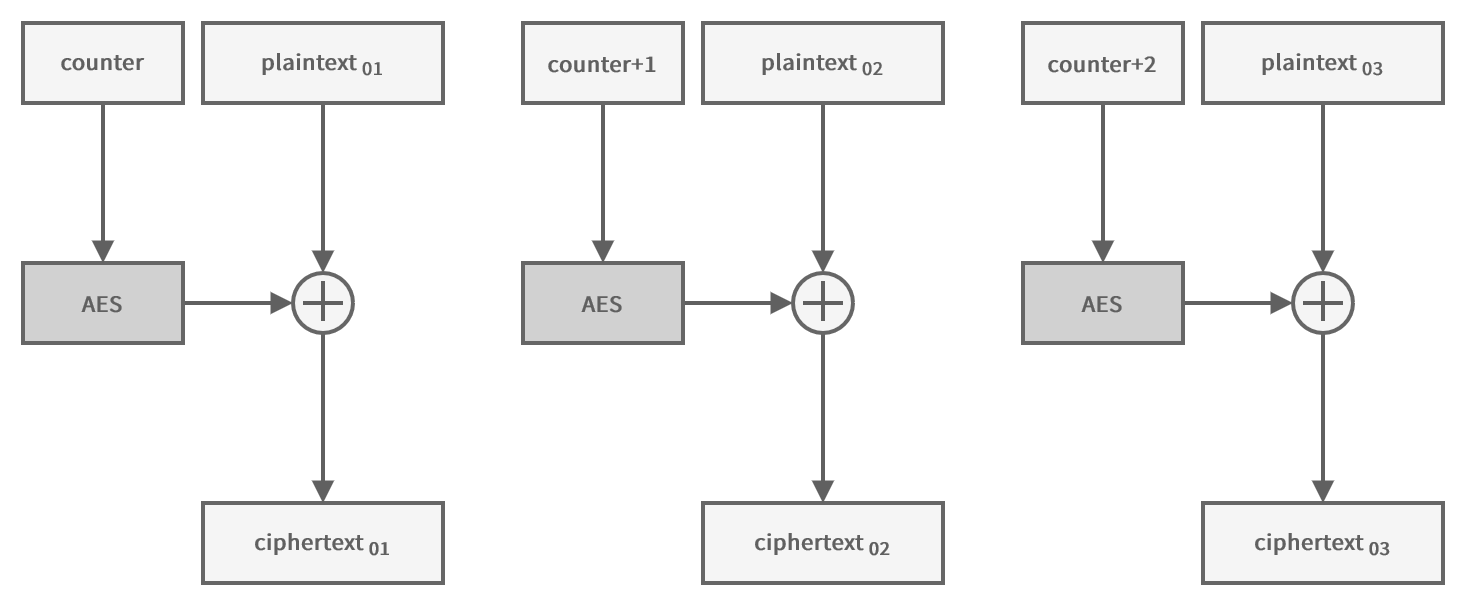
Counter (CTR)

Sometimes it is necessary to use a mode of operation that allows encrypting multiple blocks in parallel. In addition to being faster, this allows encrypting (and especially decrypting) certain parts of the message only without processing the entire message.

In this mode, the initialization vector is used as a counter, which is incremented for each block to avoid encrypting two identical blocks in the same way. The counter is encrypted and then XORed with the plaintext to produce the ciphertext.

Counter (CTR)

// AES encryption using the Counter (CTR) mode.
void aes_ctr_encrypt(AesContext *ctx, uint8_t *buffer, size_t size)
{
    // Initialize the counter from the IV
    uint8_t *counter = ctx->initialization_vector;

    // Temporary buffer for storing the encrypted counter
    uint8_t temp[16];

    // Iterate through the data in blocks of 16 bytes
    for (int i = 0; i < size; i += 16)
    {
        // Perform AES encryption on the counter
        memcpy(&temp, counter, 16);
        aes_cipher_block(ctx, (uint8_t (*)[4])temp);

        // XOR the encrypted counter with the plaintext
        for (int j = 0; j < 16 && i + j < size; j++)
            buffer[i + j] ^= temp[j];

        // Increment the counter
        for (int i = 15; i >= 0; i--)
        {
            counter[i]++;

            // Carry overflow to the next byte if necessary
            if (counter[i] != 0) break;
        }
    }
}

Because the encryption is done on the counter, which is always of a fixed size, it is not necessary to pad the plaintext.

Closing thoughts

The complete code is available here.

It’s important to note that it’s for educational purpose. It’s always better to use reputable implementations like those provided by most standard library. Even if an implementation appears to produce the correct results, it could be susceptible to side-channel attacks.

There are several other modes of operation worth exploring. For example, XEX Tweakable Block Ciphertext Stealing (XTS) is commonly used to encrypt hard drives, while Galois/Counter Mode (GCM) is used to ensure message integrity.

Finally, while this article primarily focused on the encryption process, it didn’t delve into the decryption process. However, each step of the encryption process outlined here can be easily reversed. For instance, the SubBytes step can be reversed by applying the inverse S-box, while the ShiftRows step shift the bytes to the right for decryption. To reverse the MixColumns function, we employ multiplication by the inverse matrix, and lastly, the AddRoundKey step remains unchanged during decryption.